1 基本概念

1.1 神经元 (Neure)

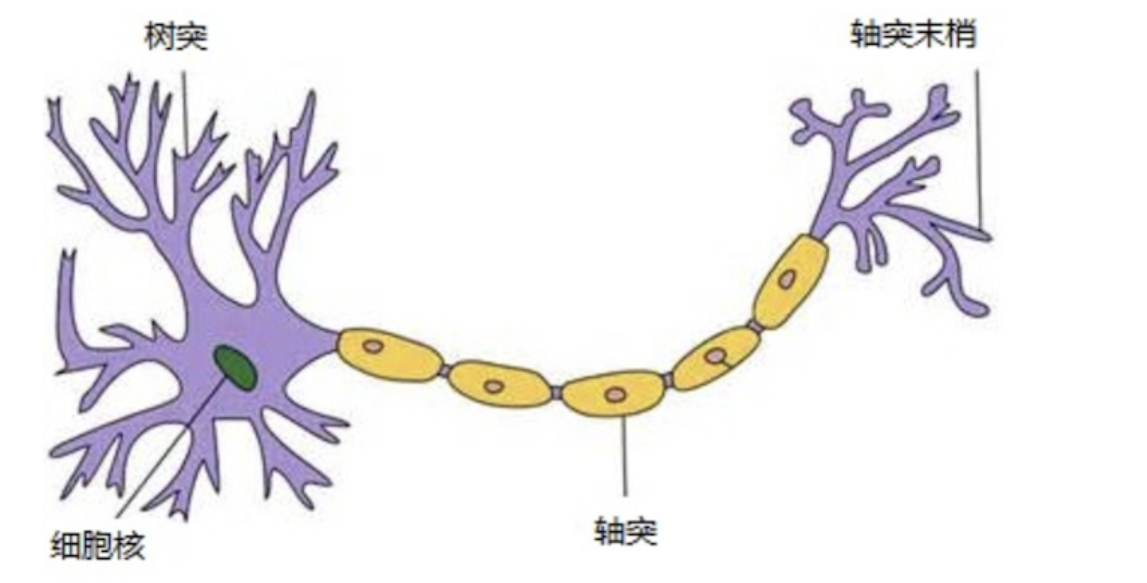
picture 0

上图是生物神经元的结构。
各个神经元传递复杂的电信号，树突接收到输入信号，然后对信号进行处理，通过轴突输出信号。
人脑可以看做是一个生物神经网络，由众多的神经元连接而成。

而下图是人工神经网络中模拟的神经元。
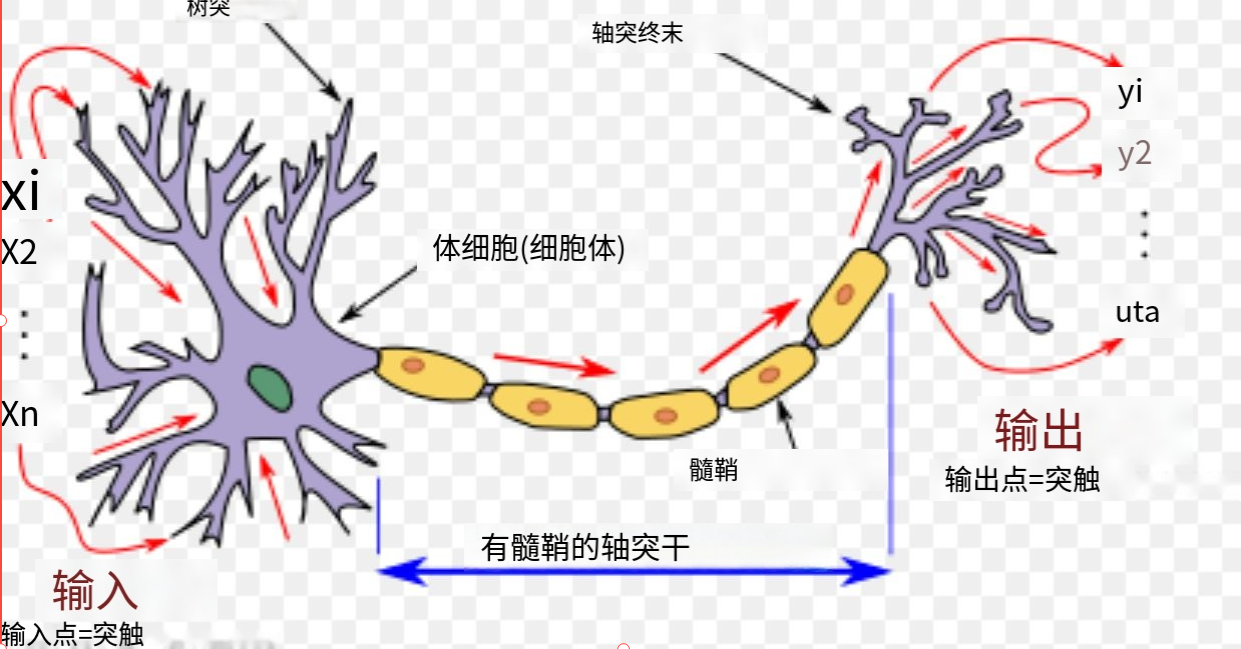
picture 1

每个人工神经元都有输入并产生单个输出，输出可发送到多个其他神经元。
输入可以是外部数据样本（如图像或文档）的特征值，也可以是其他神经元的输出。神经网络的最终输出神经元的输出完成任务。

1.2 人工神经网络 (Neural Network)

正如多个人体神经元构建了大脑，我们将多个神经元用一个圆表示，连接起来，可以构建出一个简单的人工神经网络（ Artificial Neural Network， 简写为ANN）。

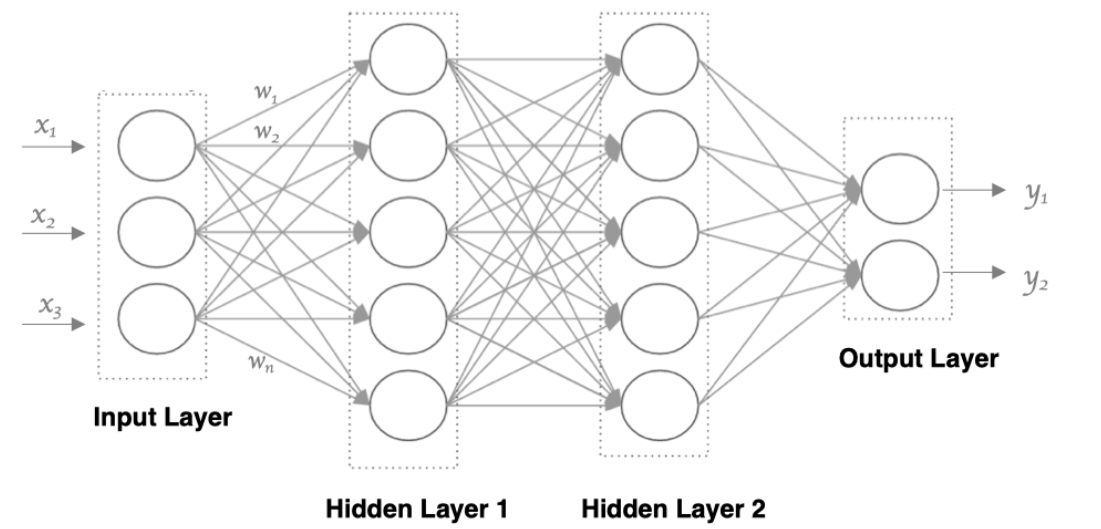
picture 2

通过上图可以看出，神经网络同一层的神经元之间没有连接。

第 N 层的每个神经元和第 N-1层 的所有神经元相连（也就是full connected（全连接））, 第N-1层神经元的输出就是第N层神经元的输入。

我们将他定义为三层结构：

  1. 输入层：由输入样本的特征值组成，通常只有一层。
  2. 隐藏层：由神经元组成，通常存在多层。
  3. 输出层：由一个神经元和输出值组成，通常存在一层。

通常，有多少个隐藏层，我们称为多少层神经网络。如上图可称为2层神经网络。

1.3 激活函数（activation function）

在上述的人工网络中，每个连接都有一个wight（权重）,其实原理就是一个线性方程(y=wx+b)。

但是神经元如果仅仅是由线性方程组成，那么无论有多少层神经网络，最终它还是一个复杂的线性方程，只能解决线性问题。

基于这个原因，我们引入了激活函数（activation function），让网络注入非线性因素，以拟合各种曲线，对每一个线性方程的结果进行激活处理，以适配更复杂的非线性场景。

所以最终，每一个神经元由一个线性方程和一个激活函数组成。

1.4 传播

正向传播(forward propagation) 是模拟人脑使用已有知识进行思考的过程，结合上列的概念，也就是数据从输入层，经过各个神经元线性计算与激活函数，最终得到输出的一个过程。

而与之对应的是 反向传播(backward propagation) ，它是模拟人脑反思更新学习的过程。通过结果反向求导，模拟人脑思考，并自动调节权重，从而加强模型达到学习目的。

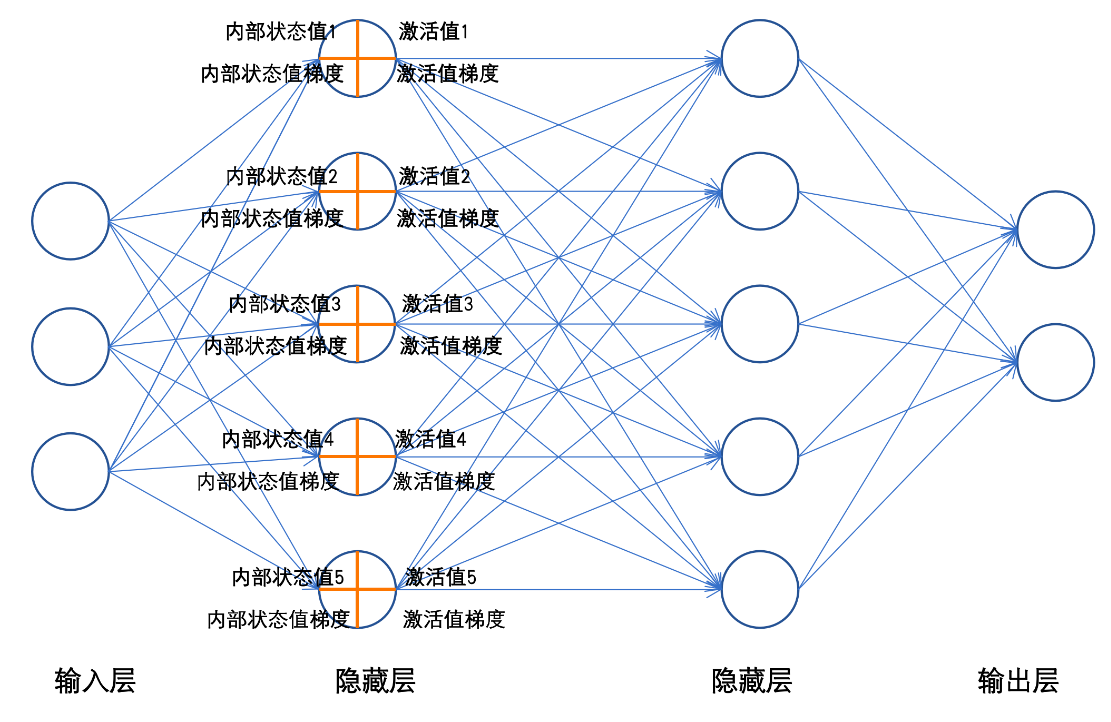
picture 3

每一个神经元工作时，前向传播会产生两个值，内部状态值和激活值；反向传播时会产生激活值梯度和内部状态值梯度。

正向传播过程：

结合上图，我们选择统一使用sigmoid激活函数，简单可以模拟一个正向传播的过程（反向传播我们将在后一章中详细讲解）：

  • 计算隐藏层1
\mathbf{Z_1} = \mathbf{X} \cdot \mathbf{W_1} + \mathbf{b_1}
\mathbf{A_1} = \sigma(\mathbf{Z_1})
即：A_{1_i} = \frac{1}{1 + e^{-Z_{1_i}}}
  • 计算隐藏层2
\mathbf{Z_2} = \mathbf{A_1} \cdot \mathbf{W_2} + \mathbf{b_2}
\mathbf{A_2} = \sigma(\mathbf{Z_2})
  • 计算输出层
\mathbf{Z_3} = \mathbf{A_2} \cdot \mathbf{W_3} + \mathbf{b_3}
Y = \mathbf{A_3} = \sigma(\mathbf{Z_3})

其中​Z_1、Z_2、Z_3为神经元的内部状态值，​A_1、A_2、A_3为神经元的激活值。

通过控制每个神经元的内部状态值、激活值的大小；每一层的内部状态值的方差、每一层的激活值的方差可让整个神经网络工作的更好。这也是优化神经网络的基础原理。

到此为止，我们了解了一个人工神经网络的基础结构和概念。以及它如何模拟人类思考，进行一个正向传播的过程，在此过程中，其它概念相对是固定的，但激活函数我们还较为陌生，后续我们将详细讲解常见的激活函数。

2 常见的激活函数

2.1 激活函数的评价

激活函数在神经网络中扮演着重要的角色，它们决定了神经元的输出，并引入非线性，使神经网络能够学习和表示复杂的函数关系。
评价一个有效的激活函数通常从以下几个方面考量：

  • 非线性（一般必须）
    激活函数需要是非线性的，以便神经网络能够表示非线性问题。如果所有的激活函数都是线性的，整个神经网络无论有多少层，也只能表示一个线性变换。
  • 可微性（必须）
    可微代表在某点可导且具备连续性。为了使用梯度下降算法进行训练，激活函数需要是可微的。这允许计算损失函数相对于权重的梯度。
  • 单调性
    一个单调的激活函数有助于确保损失函数是凸的（在一定程度上），这对于优化问题的稳定性和收敛性是有利的。
  • 输入值的范围
    激活函数的输出范围会影响梯度的稳定性。例如，Sigmoid函数的输出范围是 (0, 1)，这可能导致梯度消失问题。ReLU函数的输出范围是 [0, ∞)，这有助于缓解梯度消失问题。
  • 计算效率
    激活函数需要在计算上高效，因为在训练神经网络时，激活函数会被大量调用。高效的计算有助于加速训练过程。
  • 有效的梯度传播
    激活函数应避免导致梯度消失或梯度爆炸问题。梯度消失问题会使权重更新非常慢，而梯度爆炸问题会使权重更新过大，导致训练不稳定。

2.2 Sigmoid函数

\sigma(x) = \frac{1}{1 + e^{-x}}
  • 非线性：是
  • 可微性：是
  • 单调性：是
  • 输出范围： (0, 1)
  • 计算效率：较慢（因为有指数运算）
  • 梯度传播：可能导致梯度消失

函数图像如下：
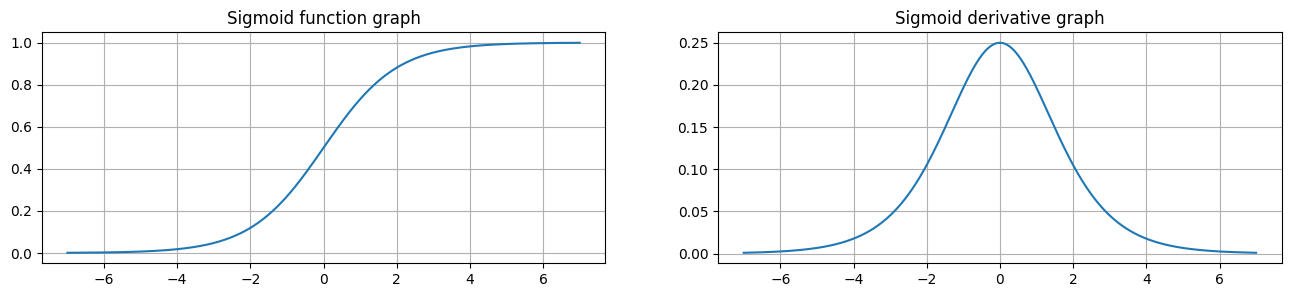
picture 4

从 sigmoid 函数图像可以得到，sigmoid 函数可以将任意的输入映射到 (0, 1) 之间，当输入的值大致在 <-5 或者 >5 时，意味着输入任何值得到的激活值都是差不多的，这样会丢失部分的信息。比如：输入 100 和输出 10000 经过 sigmoid 的激活值几乎都是等于 1 的，但是输入的数据之间相差 100 倍的信息就丢失了。

对于 sigmoid 函数而言，输入值在 [-5, 5] 之间输出值才会有明显差异，输入值在 [-3, 3] 之间才会有比较好的效果。

通过上述导数图像，我们发现导数数值范围是 (0, 0.25)，当输入 <-5 或者 >5 时，sigmoid 激活函数图像的导数接近为 0，此时网络参数将更新极其缓慢，或者无法更新。

一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象。而且，该激活函数并不是以 0 为中心的，将会导致计算收敛较慢。

所以sigmoid函数一般只用于二分类的输出层。

2.3 Tanh

\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
  • 非线性：是
  • 可微性：是
  • 单调性：是
  • 输出范围： (-1, 1)
  • 计算效率：较慢（因为有指数运算）
  • 梯度传播：相较于Sigmoid稍好，但仍可能导致梯度消失

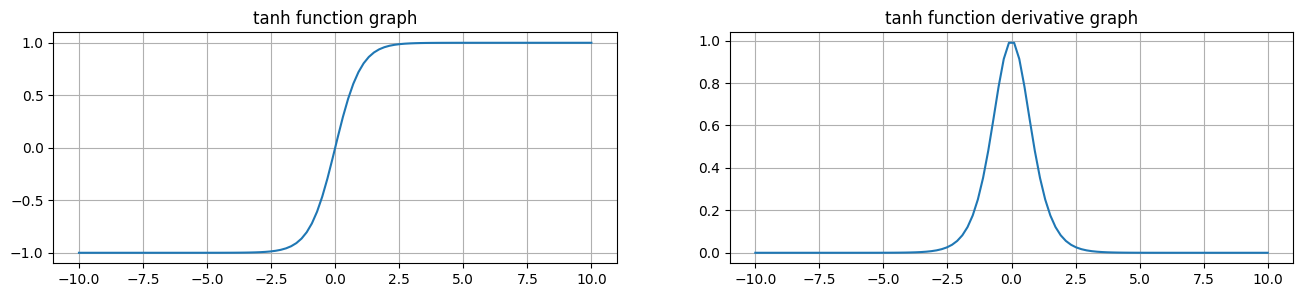
picture 5

由上面的函数图像可以看到，Tanh 函数将输入映射到 (-1, 1) 之间，图像以 0 为中心，在 0 点对称，当输入 大概<-2.5 或者 >2.5 时将被映射为 -1 或者 1。

导数值范围 (0, 1)，当输入的值大概 <-3 或者 > 3 时，其导数近似 0。

与 Sigmoid 相比，它是以 0 为中心的，使得其收敛速度要比 Sigmoid 快，减少迭代次数。

然而，从图中可以看出，Tanh 两侧的导数也为 0，同样会造成梯度消失。

Tanh使用频率较低，比较常见在递归神经网络（RNN）中使用。

2.4 ReLU

\text{ReLU}(x) = \max(0, x)
\text{ReLU}'(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x \le 0 \end{cases}
  • 非线性：是
  • 可微性：在 ​x > 0 处是，但在 ​x = 0 处不可导
  • 单调性：是
  • 输出范围： [0, ∞)
  • 计算效率：高效
  • 梯度传播：有效，减少了梯度消失问题，但可能导致“死神经元”问题

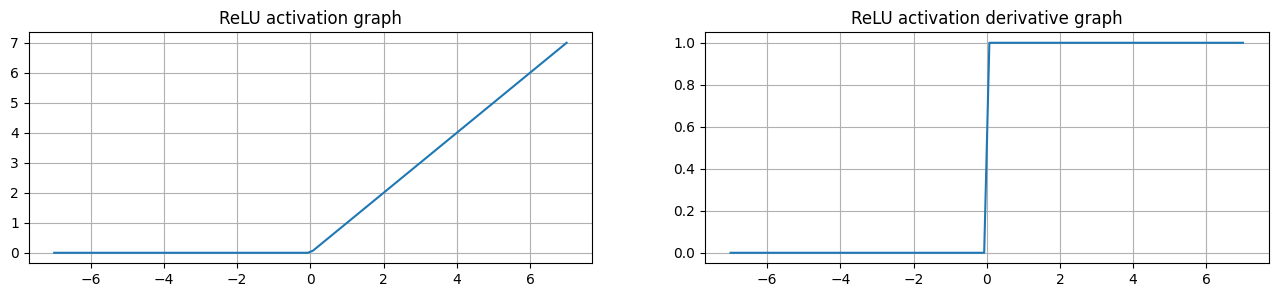
picture 6

ReLU 函数将输入映射到 [0, ∞) 之间，当输入为负数时，输出为 0，当输入为正数时，输出为输入值本身，计算相对高效。

ReLU是目前最常用的激活函数。 从图中可以看到，当x<0时，ReLU导数为0，而当x>0时，导数不存在饱和问题。所以，ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。并且导数仅有0与1，计算相对高效。

然而，随着训练的推进，部分输入会落入小于0区域，导致对应权重无法更新。这种现象被称为“神经元死亡”。
当然，神经元死亡也并非完全是坏事，在很多情况下，也缓解了过拟合问题。

2.5 Leaky ReLU

\text{Leaky ReLU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \le 0 \end{cases}
\text{Leaky ReLU}'(x) = \begin{cases} 1 & \text{if } x > 0 \\ \alpha & \text{if } x \le 0 \end{cases}
  • 非线性：是
  • 可微性：是
  • 单调性：是
  • 输出范围： (-∞, ∞)
  • 计算效率：高效
  • 梯度传播：有效，减少了死神经元问题

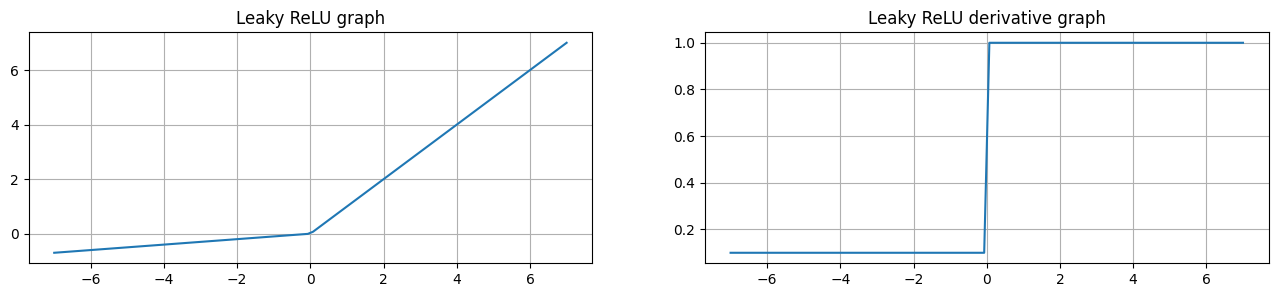
picture 7

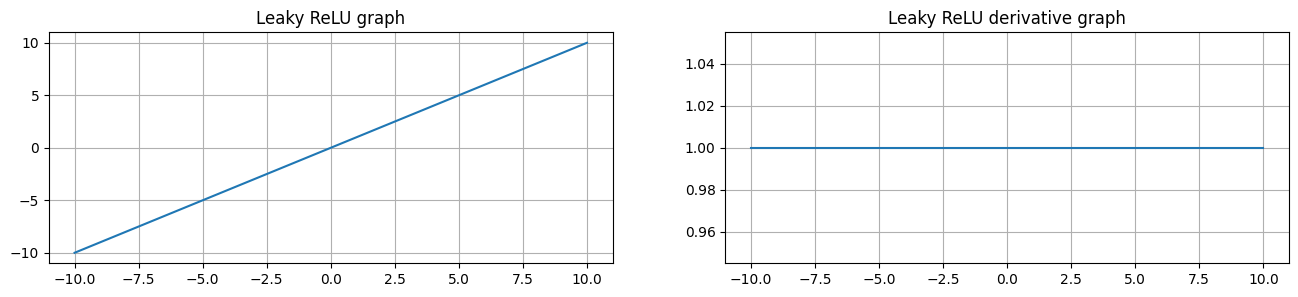
Leaky ReLU 函数是针对ReLU的优化，将输入映射到 (-∞, ∞) 之间，当输入为负数时，输出为输入值的一定比例，比如上图给的是0.01, 也就是为 -0.01x, 当输入为正数时，输出为输入值本身。

当ReLU不够理想，需要考虑避免神经元死亡时，可以使用该函数。

2.6 Softmax

\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}}

其中，​z_i 是输出层第 ​i 个神经元的输入，​K 是类别的数量。

需要注意的是，其它函数不依赖特定的损失函数。
但在实际使用中Softmax的反向传播计算通常结合了交叉熵损失函数。这是因为这种结合能够简化梯度的计算，并避免数值不稳定性。最终求导公式为：

\text{softmax}(z_i) '= \hat{y}_i - y_i
  • 非线性：是
  • 可微性：是
  • 单调性：是
  • 输出范围： [0, 1]，并且所有输出的和为1
  • 计算效率：适中，需要计算指数和归一化
  • 梯度传播：有效，适合用于反向传播

由于softmax实际使用依赖监督标签y值，所以在这里，从1到10线性模拟1000个输入，每20个有1个固定为真。则成图如下：

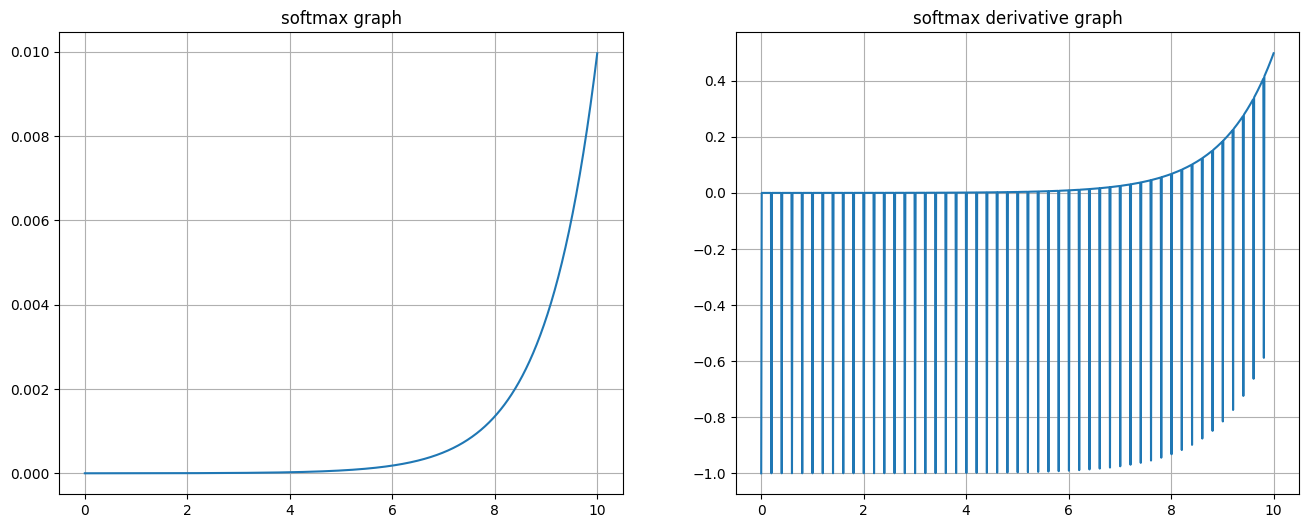
picture 9

softmax用于多分类过程中，它是二分类函数sigmoid在多分类上的推广。

它将网络的输出值转化为概率分布，确保所有输出的总和为1。这使得Softmax成为多分类任务中最常用的激活函数之一。
Softmax函数通常用于神经网络的输出层，以处理多类别分类问题。

2.7 Identity

\text{Identity}(x) = x
\text{Identity}'(x) = 1

picture 10

  • 非线性：否
  • 可微性：是，在整个定义域内可导
  • 单调性：是
  • 输出范围： (-∞, ∞)
  • 计算效率：高效
  • 梯度传播：无额外影响，梯度不会衰减或爆炸

Identity函数将输入值直接映射到输出，即输出等于输入本身。由于其简单的线性特性，计算非常高效，导数恒为1。

在回归问题中，Identity函数通常用于输出层。这是因为回归任务的目标是预测连续值，而Identity函数不会对输出值进行限制或变换。

2.8 常见激活函数抉择

  • 隐藏层:

    • 优先选择RELU激活函数
    • 如果ReLu效果不好，那么尝试其他激活，如Leaky ReLu等。
    • 如果你使用了Relu， 需要注意一下Dead Relu问题， 避免出现大的梯度从而导致过多的神经元死亡。
    • 可以尝试使用tanh激活函数，不要使用sigmoid激活函数

  • 输出层

    • 二分类问题选择sigmoid激活函数
    • 多分类问题选择softmax激活函数
    • 回归问题选择identity激活函数