1 基本概念
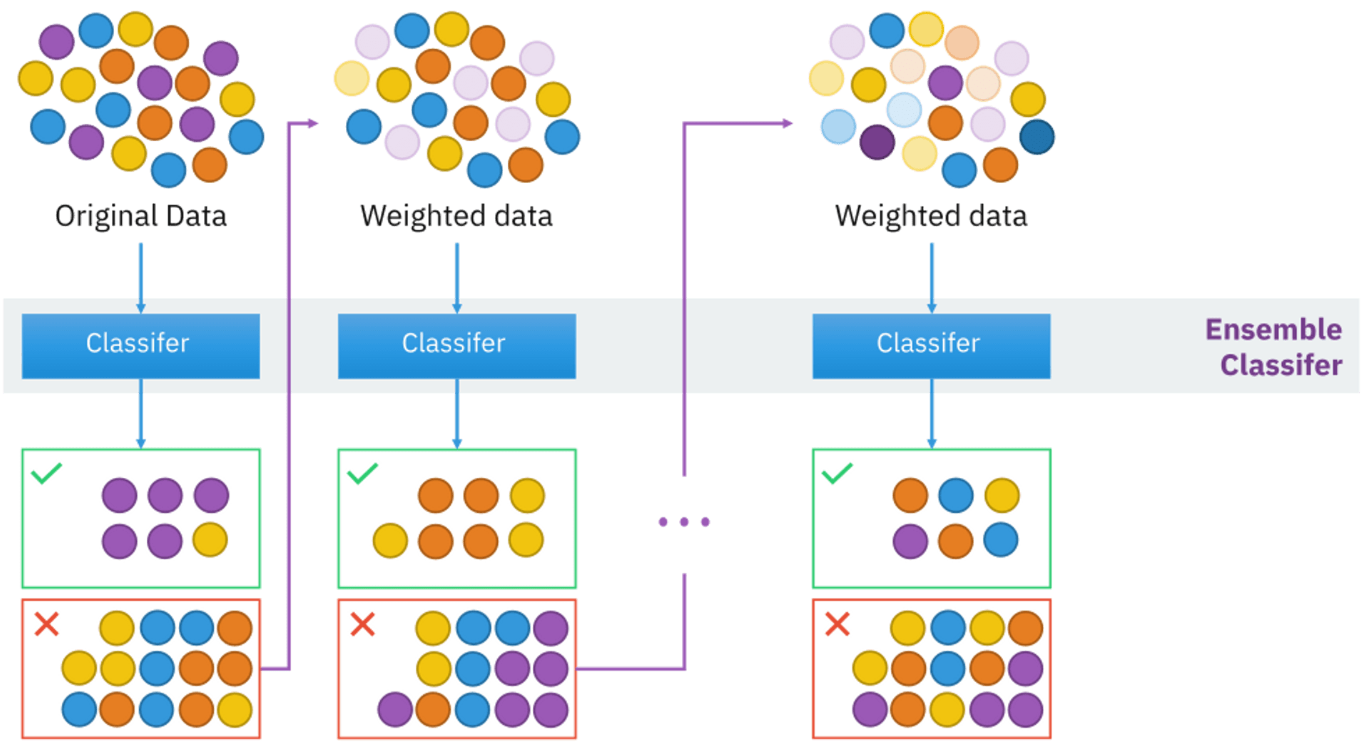
Adaptive Boosting(自适应提升),简称AdaBoost,基于 Boosting思想实现的一种集成学习算法。
它通过结合多个弱分类器(通常是决策树桩/decision stump,也就是深度为1的决策树)来形成一个强分类器,从而提高分类性能。
- 弱分类器(Weak Learner):弱分类器是指其表现略好于随机猜测的分类器。AdaBoost通过结合多个弱分类器来创建一个强分类器。
- 加权训练样本:在每一轮训练中,AdaBoost会根据上轮分类器的表现来调整训练样本的权重。错误分类的样本权重会增加,而正确分类的样本权重会减小。
- 加权弱分类器:每个弱分类器在最终分类器中的权重根据其错误率确定,错误率越低,权重越大。
- 迭代过程:AdaBoost通过多次迭代来训练多个弱分类器,每次迭代都关注之前分类错误的样本,从而逐步提高整体模型的准确性。
2. 适用场景
- 二分类问题:AdaBoost最常用于二分类问题,如垃圾邮件检测和疾病预测。当然,也可用于多分类问题,但分类不宜过多。
- 非线性数据:AdaBoost能够有效处理非线性数据,因为它通过组合多个弱分类器来捕捉数据中的复杂模式。
- 数据量适中:AdaBoost在中等大小的数据集上表现出色,太大的数据集可能会导致计算成本过高。
- 特征选择:AdaBoost可以通过调整权重来识别重要特征,从而在特征选择过程中发挥作用。
2.1 应用案例
- Viola-Jones人脸检测算法:
Viola-Jones算法通过AdaBoost结合多个简单的特征分类器,实现快速准确的人脸检测,广泛应用于数码相机、社交媒体平台和安防监控系统中。 - Gmail的垃圾邮件过滤:
Gmail使用AdaBoost来提高垃圾邮件过滤系统的准确性,通过结合多种文本特征和邮件元数据,减少垃圾邮件的误判率。 - 医疗诊断中的癌症预测:
在癌症诊断中,AdaBoost被用于结合多个基因表达特征,提高早期癌症预测的准确性,辅助医生进行诊断决策。 - 金融机构的信用评分:
金融机构使用AdaBoost模型分析客户的信用记录、交易历史等,预测客户的违约风险,帮助制定贷款决策。
3 算法构建
为了便于理解Adaboost算法,接下来我们将模拟一份简单数据,并基于决策树桩结合数学公式逐步推理。
样例数据集如下:
| 序号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | -1 | -1 | 1 | -1 |
3.1 初始化权重
首先,为每个训练样本分配一个相同的初始权重。假设训练集有N 个样本,则初始权重为:
代入样例数据后如下:
3.2 训练弱分类器
在每一轮Adaboost的迭代中,都会训练一个弱分类器,通常是一个简单的决策树桩。这个决策树桩通常是基于单一特征的简单决策规则。
如何选择特征、以及这个特征上的值,使其作为分裂点(决策边界/decision boundary),是通过最小化加权训练误差来实现的。具体步骤如下:
3.2.1 遍历特征
假设我们使用一个简单的决策树桩(一个节点的决策树)作为弱分类器。我们需要检查每个可能的阈值和每个特征。执行步骤如下:
结合本次样例,针对x的特征进行排序,确定分裂点,小于预测为1,大于预测为-1。此时我们可以进行如下思考:
-
以0.5为分裂点时,将有2项分类错误,数据如下表:
序号 1 2 3 4 5 x 0 1 2 3 4 y 1 -1 -1 1 -1 y_prediction -1 -1 -1 -1 -1 -
以1.5为分裂点,将有1项分类错误
-
以2.5为分裂点时,将有2项分类错误
-
以3.5为分裂点时,将有3项分类错误
-
以4.5为分裂点时,将有2项分类错误
3.2.2 计算加权错误并根据错误选择分裂点
对于每个可能的分裂值,计算使用该值作为决策边界时的加权错误率。这包括将数据点分类为正类或负类,并根据当前样本权重计算误分类的权重总和。
其中,\mathbb{I} 是指示函数,当h_t(x_i) \neq y_i 时取值为1,否则为0。
结合本次样例,由于是第一轮迭代,所有加权值相等恒等于0.2,可知错误项最少且最先遍历出的x=1.5 为最佳决策边界, 共有4次正确,一次错误。
| 序号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | -1 | -1 | 1 | -1 |
| y_prediction | 1 | -1 | -1 | -1 | -1 |
| w | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
3.3 计算分类器权重
这个权重将参与该分类器在最终决策计算。根据弱分类器的误差率计算其权重\alpha_t:
代入样例如下:
3.4 更新样本权重
接下来为了我们要为了下一次训练做准备,更新权重,让后续训练的分类器着重关注我们错误的部分。更新公式如下:
- w_{t+1}(i) : 第 t+1 轮迭代后第 i 个样本的新权重。
- w_t(i) : 第 t 轮迭代时第 i 个样本的当前权重。
- y_i : 第 i 个样本的实际标签。标签 y_i 通常取值为 +1 或 -1 ,表示该样本所属的类别。`
- h_t(x_i) : 第 t 个弱分类器对第 i 个样本的预测结果。预测结果 h_t(x_i) 也通常取值为 +1 或 -1 ,表示该弱分类器对该样本的预测类别。`
由于y_i 与 h_t(x_i) 的特性,我们可以理解为预测准确时,两者相乘值为-1,即权重降低,预测错误时为1,权重加强。
代入本例,计算如下:
- 对于正确分类的样本(序号1, 2, 3, 5),新的权重计算为:
- 对于错误分类的样本(序号4),新的权重计算为:
为了后续所有样本的权重总和为1,使得每个样本的权重可以被解释为一个概率值,我们要进行归一化。公式如下:
代入计算如下:
| 序号 | x | y | y预测 | 归一化后的权重 |
|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0.1 / 0.8 = 0.125 |
| 2 | 1 | -1 | -1 | 0.1 / 0.8 = 0.125 |
| 3 | 2 | -1 | -1 | 0.1 / 0.8 = 0.125 |
| 4 | 3 | 1 | -1 | 0.4 / 0.8 = 0.5 |
| 5 | 4 | -1 | -1 | 0.1 / 0.8 = 0.125 |
3.5 重复训练分类器
在2.4 中我们更新了权重,这其实就是类似回到2.1初始化权重,只不过是针对下一轮训练的。
而现在这一步就是不断循环2.2 - 2.4的步骤,直到达到预设的迭代次数或错误率不再显著改善。
这个过程的每一轮迭代都旨在不断改进模型的分类性能。
这里我们根据样例展开第二轮演示如下:
-
选择特征和分裂点
在第二轮迭代中,我们需要重新选择分裂点。我们遍历所有可能的分裂点,并计算每个分裂点的加权错误率。分裂点 错误分类数量 加权错误率 0.5 2 0.125 + 0.5 = 0.625 1.5 2 0.5 + 0.125 = 0.625 2.5 1 0.125 3.5 2 0.125 + 0.125 = 0.25 4.5 3 0.125 + 0.5 + 0.125 = 0.75 从表中可以看出,选择 x = 2.5 作为分裂点时,加权错误率最低(0.125)。
-
计算弱分类器的加权误差
对于分裂点 x = 2.5 的弱分类器 h_2(x) :
- 计算分类器权重
根据加权错误率计算当前弱分类器的权重 \alpha_2 :
- 更新样本权重
根据当前弱分类器的权重和预测结果,更新每个样本的权重:
-
对于正确分类的样本(序号1, 2, 4, 5),新的权重计算为:
w_{2}(i) = 0.125 \cdot e^{-0.97 \cdot (-1) \cdot (-1)} = 0.125 \cdot e^{-0.97} \approx 0.125 \cdot 0.379 = 0.0474 -
对于错误分类的样本(序号3),新的权重计算为:
w_{2}(3) = 0.125 \cdot e^{-0.97 \cdot (-1) \cdot (1)} = 0.125 \cdot e^{0.97} \approx 0.125 \cdot 2.64 = 0.33 -
归一化新权重,确保总和为1:
3.6 构建最终分类器
经过T 轮迭代后,将所有弱分类器组合成最终的强分类器:
-
H(x) : 最终的强分类器。它是由多个弱分类器组合而成的一个综合分类器,用于对输入 x 进行分类。
-
\text{sign} : 符号函数,定义为:
\text{sign}(z) = \begin{cases} +1 & \text{if } z > 0 \\ -1 & \text{if } z \le 0 \end{cases}这个函数决定了最终分类器的输出类别。
-
\sum_{t=1}^{T} \alpha_t \cdot h_t(x) : 所有弱分类器的加权和。其中:
- \alpha_t : 第 t 个弱分类器的权重,反映了该弱分类器的可靠性。它由该弱分类器的错误率决定,错误率越低,权重越大。
- h_t(x) : 第 t 个弱分类器对输入 x 的预测结果。通常取值为 +1 或 -1 ,表示对输入样本 x 的类别预测。
以我们之前进行的演示为例,我们进行了两轮迭代,故存在有两个弱分类器。
- 分类器1,分裂点1.5,\alpha_1=0.69
- 分类器1,分裂点2.5,\alpha_1=0.97
假设我们输入一个特征x=2进行测试,最终结果为:
到此为止,我们已经进行了完整的算法推导和演示,下一部分让我们将问题代入到python代码中实践。
4 代码实现
4.1 python函数
from sklearn.ensemble import AdaBoostClassifier
""" 用于分类"""
abc = AdaBoostClassifier(
base_estimator=None, # 基础学习器,默认为决策树桩
n_estimators=50, # 基础学习器的数量
learning_rate=1.0, # 学习率
algorithm='SAMME.R', # 提升算法类型,'SAMME'或'SAMME.R'
random_state=None # 随机种子
)
from sklearn.ensemble import AdaBoostRegressor
"""用于回归"""
abr = AdaBoostRegressor(
base_estimator=None, # 基础学习器,默认为决策树桩
n_estimators=50, # 基础学习器的数量
learning_rate=1.0, # 学习率
loss='linear', # 损失函数,'linear'、'square' 或 'exponential'
random_state=None # 随机种子
)
实际常用参数和取值:
-
base_estimator(基础学习器):- 常见取值:默认为
DecisionTreeClassifier,也可以使用其他弱学习器如SVM。 - 说明:决策树桩(单层决策树)作为基础学习器通常表现良好,可以快速训练和预测。实际使用中也可以根据具体问题选择不同的弱学习器。
- 常见取值:默认为
-
n_estimators(基础学习器的数量):- 常见取值:50到500
- 说明:更多的基础学习器可以提高模型的性能,但也会增加计算成本和过拟合风险。50到500是一个平衡点。
-
learning_rate(学习率):- 常见取值:0.01到1.0
- 说明:较低的学习率(如0.1)可以使每个基础学习器的贡献较小,从而提高模型的稳定性和性能。需要根据具体问题进行调优。
-
random_state(随机种子):
- 常见取值:整数值(如42)
- 说明:设置随机种子可以保证结果的可重复性。
-
algorithm(提升算法类型)[仅适用于分类]:- 常见取值:'SAMME.R'(默认),'SAMME'
- 说明:'SAMME.R' 使用概率提升,有时能更好地处理多分类问题。'SAMME' 适用于更传统的AdaBoost算法。'SAMME.R' 在新版sklearn中即将被淘汰。
-
loss(损失函数)[仅适用于回归]:- 常见取值:'linear'(默认),'square','exponential'
- 说明:不同的损失函数适用于不同的问题类型和数据分布。'linear' 是最常用的选择。
4.2 python代码实现
这里以sklearn的红酒数据为例,训练一个adaboost与简单的决策树对比:
"""create a adaboosting caluse on the wine dataset base on the desicion tree, the use the estimator campare with the single desicion tree"""
df_raw = load_wine(as_frame=True)
df_wine = df_raw.frame
# drop 1 type datas because original data have 3 types and adaboosting usually train on 2 types
df_wine = df_wine[df_wine['target'] != 1]
x = df_wine[['alcohol','ash','hue','proline']]
y = df_wine['target'].values
# convert the y to 0 and 1
y = LabelEncoder().fit_transform(y)
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=99)
sig_tree = DecisionTreeClassifier(criterion='entropy',max_depth=1,random_state=0)
adaboost = AdaBoostClassifier(estimator = sig_tree,n_estimators=500,learning_rate=0.1,random_state=0,algorithm='SAMME')
sig_tree.fit(x_train,y_train)
sig_tree_score = sig_tree.score(x_test,y_test)
print(f"sig_tree_score = {sig_tree_score}")
adaboost.fit(x_train,y_train)
adaboost_score = adaboost.score(x_test,y_test)
print(f"adaboost_score = {adaboost_score}")